Machine learning expands prediction capacity in complex, chaotic systems
Framework may one day be relevant for COVID-19 prediction

Just as a neurologist looks to a patient’s neural network for guidance in addressing neurodegenerative diseases like Parkinson’s, Alzheimer’s and Huntington’s, researchers in the artificial intelligence arena study neural networks (composed of artificial neurons) to improve predictability in complex physical, biological and engineering systems.
Arizona State University’s Ying-Cheng Lai, a professor of electrical engineering and physics, and his team combine expertise in chaos theory, physics, applied mathematics and engineering to develop model-free, purely data-driven machine learning frameworks to predict chaotic systems.
In a new paper for Physical Review Research titled “Long-term prediction of chaotic systems with machine learning,” Lai and his team use artificial recurrent neural networks to increase the ability to predict the state changes and evolution in chaotic systems that exhibit a sensitive dependence on initial conditions.
Chaos is often exemplified as the mechanism behind the “Butterfly Effect,” wherein a butterfly flapping its wings may cause a seemingly unpredictable, catastrophic weather event half a world away.
“In a chaotic system, you cannot make a long-term prediction,” explained Lai, “because a small amount of error is going to be magnified exponentially.”
Machine learning is now making long-term predictions more attainable.
“It’s an incremental process,” Lai said. “We train the neural machine with measured time series from the chaotic system of interest, such as an electrical power system, a nonlinear optical system or an epidemiological system such as the spread of COVID-19, and the machine begins to gain the ability to predict the future of the system."
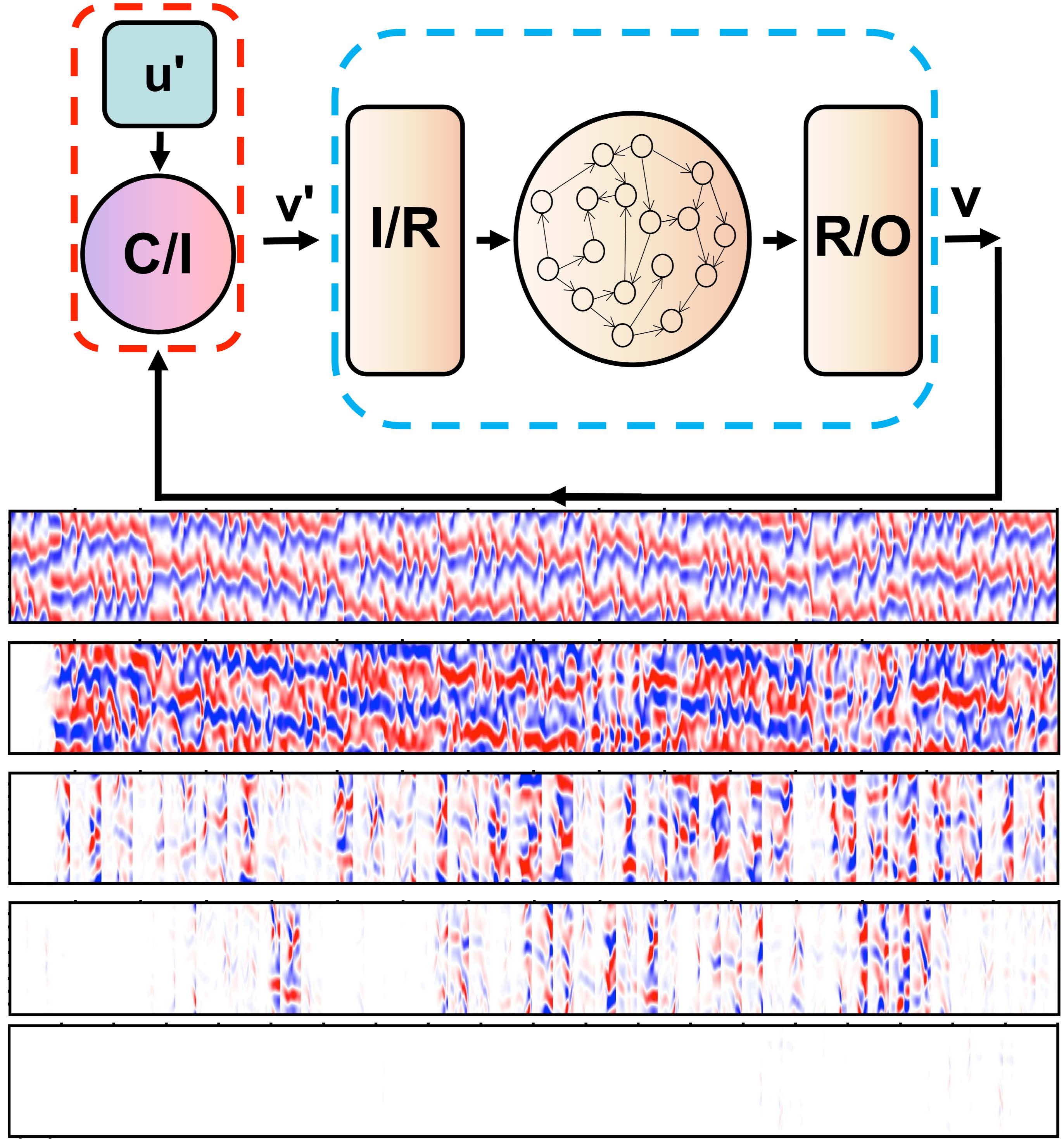
A neural network machine so trained is able to predict the state evolution of a chaotic system five or six times longer than that which can be achieved using the traditional prediction methods in nonlinear dynamics.
Yet, because of the nature of chaos, prediction will begin to deteriorate over time. Additional data is then added to lengthen the prediction time horizon.
“We add one or two data points once every few cycles of natural oscillation of the system to gradually update the knowledge base of the machine so that it can keep generating accurate predictions for an arbitrary, long period of time,” Lai said.
Top: Articulate neural network structure for long-term prediction of chaotic systems. Panel 2: Spatiotemporal state evolution of a chaotic system, where the ordinate is space and the abscissa indicates time. Panel 3: Prediction errors without state update (the white region indicates near zero error). Panels four through six: As rare state updates are provided to the machine at an increasing rate, the prediction errors are reduced and eventually diminish in space and time.
Lai’s group is currently working on exploiting machine learning to predict catastrophic events in complex systems. For example, if you train a machine with data from an ecosystem in a normal functioning regime before any collapse, the machine has the power to predict, upon some changes in the environment, if and when the system is going to collapse.
Likewise, the machine will ultimately be able to predict interruptions to a power grid.
“We can train the machine to virtually mimic previous failures,” Lai said. “We can measure voltage usage at certain points and, based on historical grid failures, identify if and when the grid may be vulnerable to failure.”
With regard to COVID-19, Lai notes that one challenge is that the currently available datasets are still too small to train a machine. However, people have used data from the SARS epidemic in 2003–04 for training to predict the current COVID-19 trend.
“At the moment, it seems that machine learning may be of secondary importance because a detailed and comprehensive mathematical model for COVID-19 can be built, which has generated accurate predictions of the epidemic trends in China, South Korea, Italy and Iran.”
Other researchers who contributed to this work are Huwei Fan, Junjie Jiang, Chun Zhang and Xingang Wang. In addition to their affiliations with ASU, Fan and Zhang are also affiliated with the School of Physics and Information Technology at Shaanxi Normal University, Xi’an, China.
More Science and technology
ASU author puts the fun in preparing for the apocalypse
The idea of an apocalypse was once only the stuff of science fiction — like in “Dawn of the Dead” or “I Am Legend.” However these days, amid escalating global conflicts and the prospect of a nuclear…

Meet student researchers solving real-world challenges
Developing sustainable solar energy solutions, deploying fungi to support soils affected by wildfire, making space education more accessible and using machine learning for semiconductor material…

Miss Arizona, computer science major wants to inspire children to combine code and creativity
Editor’s note: This story is part of a series of profiles of notable spring 2024 graduates. “It’s bittersweet.” That’s how Tiffany Ticlo describes reaching this milestone. In May, she will graduate…